RESISTANCE DES MATERIAUX FLEXION // lien pour téléchargement http://scapognel.com/flp

RESISTANCE DES MATERIAUX FLEXION

RESISTANCE DES MATERIAUX

Schématisation des liaisons

Dans le cas des problèmes plans (systèmes de forces coplanaires), la schématisation des liaisons et des efforts exercés se ramène à trois cas types : appui simple (ponctuel ou plan sans frottement), articulation (pivot) et encastrement.

Efforts intérieurs

Dans le cas de la flexion, les efforts intérieurs dans n’importe quelle section droite se réduisent à un effort tranchant T (perpendiculaire à la ligne moyenne) et à un moment fléchissant Mf (perpendiculaire à la ligne moyenne et à T).

Pour faire apparaître les efforts intérieurs, on effectue une coupure fictive à la distance x de l’origine A. En isolant le tronçon 1, on obtient l’effort tranchant T et le moment fléchissant Mf (on obtient en fait respectivement –T et –Mf, voir Cours « Torseur de Cohésion »).

T= somme vectorielle de toutes les forces extérieures transversales situées à gauche de la section fictive = ( F1+ F2 )

M f = moment résultant en G de toutes les actions extérieures situées à gauche de la section fictive 

Diagrammes

Les valeurs de l’effort tranchant T et du moment fléchissant Mf varient avec la position x de la coupure fictive. Les diagrammes de t et Mf (graphes mathématiques de type (x, y)) permettent de décrire les variations de ces deux grandeurs et ainsi repérer les maximums à prendre en compte lors des calculs des contraintes.

Essai de flexion

Un dispositif de mise en charge exerce une poussée de 20 000 N qui se répartit en C et D, alors que le

bâti de la machine supporte la poutre en A et B. La symétrie du chargement et des appuis entraîne A=

B = C = D = P = 10 000 N, le poids de la poutre étant négligé.

Poutre encastrée

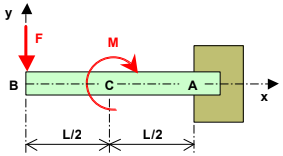
On considère une poutre encastrée de longueur L = 2 m soumise à un effort concentré F = 1 000 N (vers le bas) au point B et à un couple pur M = 1 000 Nm (sens antitrigonométrique) autour du point C.

Charges réparties

Les charges réparties ont pour origine les actions de pesanteur et des actions de contact diverses (vent,neige, pression d’un fluide...). Elles peuvent être uniformes ou variables.

Charge répartie linéairement variable

Nous allons également traiter ce cas à partir d’un exemple. Prenons le cas d’une poutre (longueur L = 3 m) encastrée en A, supportant la charge linéairement croissante q(x) de la figure ci-contre.

Contraintes de flexion

En flexion, les contraintes normales s sont généralement prépondérantes devant les contraintes de

cisaillement t.

Contraintes normales en flexion

Les contraintes normales résultent du moment fléchissant Mf (les efforts tranchants n’ont aucun effet sur leur valeur). Dans le cas de flexion pure (  M f différent de 0 et T = 0), les poutres se déforment suivant des arcs de cercles.

La ligne moyenne GG’ ne subit ni allongement ni raccourcissement (contraintes s nulles).

Pour la figure proposée, les fibres situées au-dessus de la ligne neutre sont comprimées et supportent des contraintes de compression ; celles situées au-dessous (MM’) sont tendues et supportent des contraintes de traction.

En exprimant l’allongement de la fibre MM’, en utilisant la loi de Hooke (s = E e ) et en faisant intervenir le moment fléchissant Mf, 

Exemple : 

déterminons les contraintes normales dans une poutre rectangulaire (50 mm / 120 mm), soumise à un moment fléchissant de 14.4 kNm constant sur toute sa longueur.

Calcul des constructions

Pour des questions de sécurité liées à l’usage des machines, la contrainte normale s Maxi dans la section droite la plus chargée doit rester inférieure à une contrainte limite admissible liée au matériau et fixée par le constructeur ou par des normes : Rpe. Dans le cas précis de la flexion, il faut donc procéder ainsi :

• v commencer par déterminer la section la plus chargée (en général celle où le moment fléchissant est maximum) ;
• v puis vérifier que la contrainte maximale dans cette section est inférieure à la contrainte admissible Rpe imposée par le constructeur.

Exemple : 

une poutre de pont roulant (profilé IPE) est soumise aux charges indiquées sur la figure ci-dessous (cas le plus défavorables). Le moment fléchissant maximum est obtenu au milieu de la poutre et a pour valeur 110 kNm (vous auriez pu le déterminer facilement, mais là n’est pas le problème). Si on impose une contrainte admissible de 100 MPa, déterminons le profilé pouvant convenir pour construire l’appareil.

lien pour téléchargement

http://scapognel.com/flp