Application de la méthode des forces // Lien de téléchargement : http://scapognel.com/1jov

Application de la méthode des forces

INTRODUCTION

Les poutres continues sont des structures qu'on rencontre très fréquemment dans les constructions courantes. On appelle poutre continue une poutre reposant sur plusieurs appuis.

Il s’agit généralement d’appuis simples, à l’exception d’un seul qui est un appui double et dont le rôle consiste à assurer la stabilité géométrique de la poutre, comme empêcher la translation horizontale dans le cas de la figure ci-dessous .

L’appui double peut être placé à une extrémité ou, plus généralement, être un appui intermédiaire.

Les extrémités d’une poutre continue peuvent très bien comporter des porte-

à-faux ou être encastrées. Le traitement de ces cas particuliers est abordé plus loin.

Les poutres continues sont des systèmes hyperstatiques puisqu’elles présentent des liaisons surabondantes (toutes les liaisons en plus de ce que doit comporter une poutre isostatique). Dans le cas d’une poutre sans encastrements, le

nombre de liaisons surabondantes, donc le degré d’hyperstaticité, est égal au nombre d’appuis intermédiaires.

Comparativement à une série de poutres bi-articulées dont le nombre est égal à celui des travées d’une poutre continue, cette dernière est plus économique car es moments fléchissants qui la sollicitent sont plus faibles. La comparaison est encore plus nettement à l’avantage de la poutre continue par rapport à une poutre isostatique unique de même longueur. Dans une poutre continue, les appuis intermédiaires contribuent à réduire et à mieux répartir sur toute la poutre le moment fléchissant (qui est la sollicitation prépondérante). Cette observation reste valable pour les déplacements qui sont nettement moins importants dans le cas des poutres continues.

Ces dernières présentent par ailleurs une plus grande rigidité et résistent de ce fait mieux à l’action dynamique. Les charges considérées ici sont supposées être appliquées statiquement. Elles sont constituées de charges transversales (voire inclinées), concentrées ou réparties, et de couples. Contrairement aux poutres isostatiques, les poutres continues, comme tous les systèmes hyperstatiques, sont très sensibles aux déplacements des appuis. Ce phénomène a déjà été mis en exergue dans un exemple d’application des formules de Bresse traitant une poutre continue soumise au seul effet de l’affaissement d’un de ses appuis. Lorsque des tassements d’appuis sont à craindre, les poutres isostatiques sont mieux indiquées. Si pour quelque raison que ce soit des appuis intermédiaires sont nécessaires, on ajoute à la poutre continue des articulations judicieusement placées de manière à la rendre isostatique et annuler ainsi sa sensibilité aux affaissements des appuis susceptibles de se produire. Ce type de poutre - poutre reposant sur plusieurs appuis et rendue isostatique par l’ajout de rotules - est désigné par poutre Gerber. Elles sont obtenues en ajoutant autant d’articulations qu’il y a d’appuis intermédiaires. Pour s’assurer que la structure obtenue est bien isostatique et qu’il n’y a ni tronçon déformable (tronçon libre constituant un mécanisme) ni tronçon hyperstatique, il suffit de respecter la règle suivante : pas plus de deux articulations entre deux appuis, ni plus de deux appuis entre deux articulations. A titre d’exemple

L’influence du moment fléchissant sur les déformations étant prépondérante dans les poutres continues, c’est la seule sollicitation dont il sera tenu compte lors du calcul des déplacements que nous serons amenés à effectuer.

APPLICATION DIRECTE DE LA METHODE DES FORCES

Considérons une poutre continue horizontale sans encastrements . L'application directe et intuitive de la méthode des forces conduit à considérer comme inconnues hyperstatiques les réactions (verticales) des appuis intermédiaires.

Cependant, ce choix n’est pas intéressant car il implique des calculs fastidieux à cause notamment du fait que les moments msk et MsF sont généralement différents de zéro sur toute la longueur de la poutre. De la sorte, les éléments de la matrice de souplesse [δ u ] et du vecteur déplacement [δF] sont tous non nuls. Ceci n’est pas la seule raison ; il en existe une autre plus déterminante. Chaque colonne de la matrice [δ u ] représente les déplacements (flèches s’il s’agit d’une poutre horizontale) des points d’application des inconnues hyperstatiques provoqués par une sollicitation unitaire. Pour une poutre comportant plusieurs appuis intermédiaires, deux colonnes successives de [δ u ] auront des valeurs très proches et seront comparables. De ce fait, la matrice [δ u ] devient pratiquement singulière et conduit à des solutions très imprécises lors de la résolution du système d’équations canoniques. Aussi, on opte pour un autre choix des inconnues hyperstatiques de manière à contourner cette difficulté et à réduire les calculs.

FORMULE DES TROIS MOMENTS :

Etablissement de la formule Considérons une poutre continue sans encastrements à n travées. Son degré d'hyperstaticité est égal à n-1

Prenons pour inconnues hyperstatiques les moments fléchissants agissant au droit de chaque appui intermédiaire.

Pour ce faire, on procède à des coupures de manière à supprimer la liaison de moment au niveau de chaque appui. S’agissant d’inconnues hyperstatiques internes, chaque coupure libère deux inconnues (des moments) égales est opposées. En pratique, cela revient à introduire une articulation au-dessus de chaque appui intermédiaire .

Pour remplacer les liaisons supprimer, on applique aux lèvres de chacune des coupures deux couples égaux et opposés (M1 , M2 , …, Mn-1)

Le système statique de base ainsi obtenu présente une propriété remarquable. En effet, on remarque que si on charge une travée, les autres ne subissent aucune influence. Ce résultat signifie que le système principal se comporte comme une succession de poutres simplement appuyées obtenues par séparation des n travées.

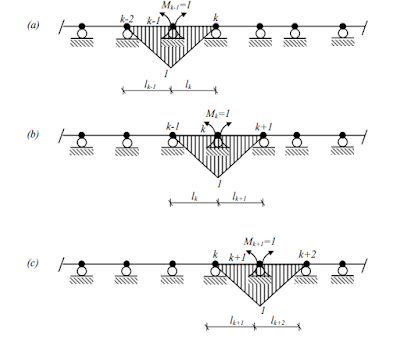
Calcul des coefficients de la formule des trois moments

Il reste à calculer les coefficients intervenant dans l'équation . Considérons une poutre continue sans encastrement comportant n travées. Les diagrammes unitaires permettant le calcul des coefficients , et sont représentés